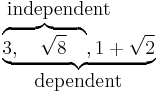
Rational dependence

In mathematics, a collection of real numbers is rationally independent if none of them can be written as a linear combination of the other numbers in the collection with rational coefficients. A collection of numbers which is not rationally independent is called rationally dependent. For instance we have the following example.

$\begin{matrix} \mbox{independent}\qquad\\ \underbrace{ \overbrace{ 3,\quad \sqrt{8}\quad }, 1%2B\sqrt{2} }\\ \mbox{dependent}\\ \end{matrix}$

Formal definition

The real numbers ω₁, ω₂, ... , ω_n are said to be rationally dependent if there exist integers k₁, k₂, ... , k_n not all zero, such that

$k_1 \omega_1 %2B k_2 \omega_2 %2B \cdots %2B k_n \omega_n = 0.$

If such integers do not exist, then the vectors are said to be rationally independent. This condition can be reformulated as follows: ω₁, ω₂, ... , ω_n are rationally independent if whenever k₁, k₂, ... , k_n are integers such that

$k_1 \omega_1 %2B k_2 \omega_2 %2B \cdots %2B k_n \omega_n = 0.$

we have k_i = 0 for i = 1, 2, ..., n, i.e. only the trivial solution exists on the integers. Note that if we consider the reals as a vector space over the rationals, this is just the usual definition of linear independence.

Bibliography

Anatole Katok and Boris Hasselblatt (1996). Introduction to the modern theory of dynamical systems. Cambridge. ISBN 0-521-57557-5.

‹The stub template below has been proposed for renaming to . See stub types for deletion to help reach a consensus on what to do.
Feel free to edit the template, but the template must not be blanked, and this notice must not be removed, until the discussion is closed. For more information, read the guide to deletion.›

Rational dependence

Formal definition

See also

Bibliography